柏林噪声是一种特殊的随机噪声，即对于每个给定的值产生的随机数是唯一的，但是不同的

值产生不同的随机数。关于柏林噪声更详细的解释可以参考这里：

 

本文主要是探讨如何使用柏林噪声产生火焰效果与乌云效果的纹理，在解释实现代码之前，

首先来看一下影响柏林噪声效果的两个参数音度(Octave) 与余辉(Persistence)，可以调节

纹理的大小和密度。

 

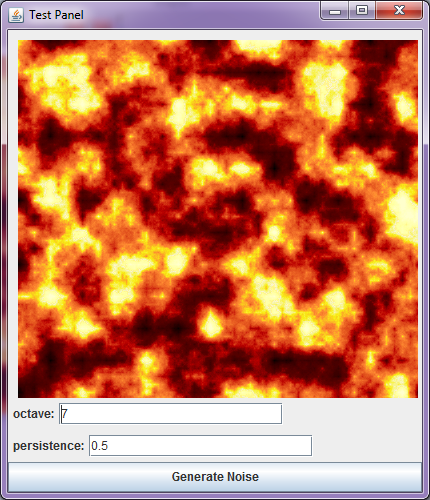
最终实现的火焰纹理效果

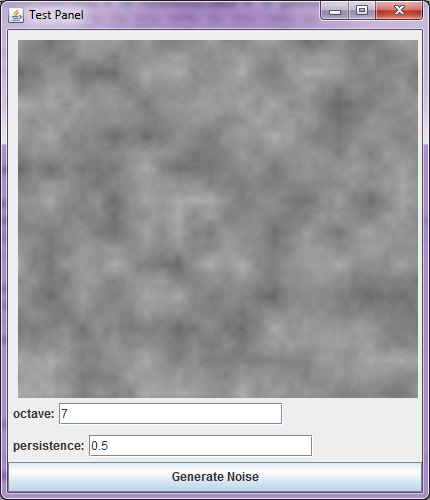
最终实现的乌云纹理效果

最终实现的草地纹理效果–怎么感觉有点魔兽中精灵族的草地啊，哈哈

代码解释

首先产生随机空白噪声，使用随机空白噪声产生柏林噪声，最后将柏林噪声映射为RGB值

输出到指定大小的图像中，代码如下:

float[][] whiteNoise = GenerateWhiteNoise(rows, cols);

float[][] perlinNoise = GeneratePerlinNoise(whiteNoise, 6); //

float[][] colorData = MapGray(perlinNoise);

 

白噪声产生主要是利用JAVA中的系统时间作为种子，产生[0~1]之间的噪声数组

代码如下：

public float[][] GenerateWhiteNoise(int width, int height)

{

Random random = new Random(System.currentTimeMillis());    

float[][] noise = new float[width][height];

for (int i = 0; i < width; i++)

{

        for (int j = 0; j <height; j++)

        {

            noise[i][j] = (float)random.nextDouble();

        }

    }

    return noise;

}

 

柏林噪声的产生稍微复杂一点点，首先把上面的白噪声数据带入，利用插值公式产生平滑的噪声

数据，具体要产生几组平滑噪声数据取决于音度(Octave)参数。本程序的插值公式非常简单，

代码如下：

public float Interpolate(float x0, float x1, float alpha)

{

return x0 * (1 - alpha) + alpha * x1;

}

最后把这些组的平滑噪声加上不同的振幅混合在一起产生一个输出数组结果即为柏林噪声。

完成上面这些还不足以产生那些效果震撼的纹理，另外一个顶级秘诀在于怎么把柏林噪声

映射到你想要的RGB值。代码如下：

    float[][] MapGradient(float[][] perlinNoise)

    {

       int width =perlinNoise.length;

       int height =perlinNoise[0].length;

       float[][] image = new float[width][height];

       int ta=0, tr=0, tb=0,tg=0;

       for (int i = 0; i <width; i++)

       {

          for (int j = 0; j <height; j++)

          {

          ta = 255;

          int u = (int)(perlinNoise[i][j] * (float)angryFireColorTable.length);

          tr = (int)angryFireColorTable[u][0];

          tg = (int)angryFireColorTable[u][1];

          tb = (int)angryFireColorTable[u][2];

          image[i][j] = (ta <<24) | (tr << 16) | (tg << 8) | tb;

          }

       }

      

       return image;

    }

程序完全源代码如下：

package com.gloomyfish.perlin.noise;  import java.util.Random;  public class PerlinNoiseCreator { 	 	private int[][] angryFireColorTable = { 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204}, 			{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 204},	{255, 255, 199},	 			{255, 255, 199},	{255, 255, 197},	{255, 255, 197},	{255, 255, 193},	{255, 255, 193}, 			{255, 255, 191},	{255, 255, 191},	{255, 255, 189},	{255, 255, 189},	{255, 255, 185}, 			{255, 255, 185},	{255, 255, 183},	{255, 255, 183},	{255, 255, 179},	{255, 255, 179}, 			{255, 255, 177},	{255, 255, 177},	{255, 255, 175},	{255, 255, 175},	{255, 255, 171},		 			{255, 255, 171},	{255, 255, 169},	{255, 255, 169},	{255, 255, 167},	{255, 255, 167}, 			{255, 255, 163},	{255, 255, 161},	{255, 255, 157},	{255, 255, 155},	{255, 255, 153}, 			{255, 251, 149},	{255, 249, 147},	{255, 246, 144},	{255, 244, 142},	{255, 242, 140}, 			{253, 244, 205},	{248, 246, 197},	{248, 246, 187},	{248, 245, 178},	{248, 245, 168}, 			{247, 245, 160},	{248, 243, 149},	{247, 244, 141},	{249, 243, 133},	{248, 243, 123}, 			{249, 242, 112},	{248, 242, 102},	{248, 242, 92},	{247, 241, 81},	{248, 241, 73}, 			{247, 240, 63},	{249, 239, 53},	{247, 239, 42},	{249, 238, 32},	{249, 238, 26}, 			{248, 234, 21},	{248, 231, 21},	{250, 224, 25},	{248, 218, 24},	{249, 214, 26}, 			{249, 209, 26},	{252, 204, 32},	{251, 198, 32},	{251, 191, 33},	{251, 186, 34}, 			{250, 179, 35},	{252, 176, 38},	{252, 169, 41},	{252, 164, 41},	{254, 157, 44}, 			{254, 151, 46},	{253, 145, 47},	{254, 141, 49},	{251, 136, 47},	{253, 135, 48}, 			{251, 130, 47},	{250, 129, 46},	{249, 126, 46},	{247, 124, 44},	{246, 120, 43}, 			{244, 118, 41},	{243, 115, 42},	{241, 113, 40},	{242, 111, 41},	{240, 109, 39}, 			{239, 104, 40},	{236, 101, 37},	{234, 99, 35},	{235, 97, 34},	{232, 93, 34}, 			{231, 91, 32},	{229, 88, 32},	{227, 86, 30},	{227, 83, 30},	{225, 81, 28}, 			{224, 78, 27},	{222, 76, 25},	{223, 72, 27},	{221, 70, 25},	{219, 66, 24}, 			{216, 63, 22},	{216, 58, 21},	{212, 54, 19},	{210, 50, 18},	{209, 45, 17}, 			{206, 40, 14},	{206, 37, 14},	{203, 32, 12},	{200, 29, 9},	{200, 24, 9}, 			{197, 21, 6},	{195, 17, 7},	{191, 13, 3},	{190, 7, 3},	{188, 5, 1}, 			{184, 2, 0},	{180, 0, 0},	{178, 0, 0},	{174, 0, 0},	{172, 0, 0}, 			{169, 1, 0},	{164, 0, 1},	{160, 0, 0},	{158, 0, 0},	{154, 0, 0}, 			{150, 0, 0},	{146, 0, 0},	{144, 0, 0},	{140, 0, 1},	{136, 0, 2}, 			{133, 0, 1},	{130, 0, 0},	{126, 1, 0},	{124, 0, 2},	{120, 0, 1}, 			{116, 0, 0},	{112, 0, 0},	{109, 1, 1},	{104, 0, 0},	{103, 0, 1}, 			{98, 0, 0},	{95, 0, 0},	{92, 1, 0},	{92, 1, 0},	{90, 0, 0}, 			{89, 1, 0},	{88, 0, 0},	{86, 0, 0},	{86, 0, 0},	{84, 0, 0}, 			{84, 0, 0},	{82, 1, 0},	{82, 1, 0},	{80, 0, 0},	{80, 0, 0}, 			{79, 1, 1},	{78, 0, 0},	{76, 0, 0},	{76, 0, 0},	{74, 0, 0}, 			{74, 0, 0},	{72, 0, 1},	{72, 0, 1},	{70, 0, 0},	{70, 0, 0}, 			{69, 1, 2},	{68, 0, 1},	{66, 0, 1},	{66, 0, 1},	{64, 0, 0}, 			{62, 1, 0},	{61, 1, 1},	{60, 0, 0},	{60, 0, 0},	{60, 0, 0}, 			{58, 0, 0},	{58, 0, 0},	{56, 0, 1},	{56, 0, 1},	{54, 0, 0}, 			{54, 0, 0},	{52, 1, 0},	{51, 0, 0},	{50, 0, 1},	{50, 0, 1}, 			{49, 1, 1},	{48, 0, 0},	{46, 0, 0},	{46, 0, 0},	{44, 0, 1}, 			{42, 0, 1},	{42, 0, 1},	{40, 0, 0},	{40, 0, 0},	{39, 0, 0}, 			{38, 0, 0},	{38, 0, 0},	{36, 0, 0},	{35, 0, 0},	{34, 0, 0}, 			{34, 0, 0},	{32, 0, 1},	{30, 0, 0},	{30, 0, 0},	{29, 1, 0}, 			{28, 0, 0},	{28, 0, 0},	{26, 0, 1},	{24, 0, 0},	{22, 1, 0}, 			{22, 1, 0},	{21, 1, 0},	{20, 0, 0},	{19, 1, 1},	{19, 1, 1}, 			{16, 0, 0},	{16, 0, 0},	{16, 0, 0},	{14, 0, 0},	{12, 0, 0}, 			{12, 0, 0},	{11, 1, 0},	{10, 0, 0},	{9, 1, 0},	{8, 0, 0}, 			{6, 0, 0},	{6, 0, 0},	{5, 1, 0},	{4, 0, 0},	{2, 1, 0}, 			{2, 1, 0},	{1, 1, 1},	{0, 0, 0},	{0, 0, 0},	{0, 0, 0}, 		};  	 	public void generateNoise(int[] noiseData, int rows, int cols) {  		float[][] whiteNoise = GenerateWhiteNoise(rows, cols); 		float[][] perlinNoise = GeneratePerlinNoise(whiteNoise, 6); // default value is 6 		//float[][] colorData = MapGradient(perlinNoise); 		float[][] colorData = MapGray(perlinNoise); 		int index = 0; 		for(int row = 0; row
     
      << octave; // calculates 2 ^ k 	   float sampleFrequency = 1.0f / samplePeriod; 	  	   for (int i = 0; i < width; i++) 	   { 	      //calculate the horizontal sampling indices 	      int sample_i0 = (i / samplePeriod) * samplePeriod; 	      int sample_i1 = (sample_i0 + samplePeriod) % width; //wrap around 	      float horizontal_blend = (i - sample_i0) * sampleFrequency; 	  	      for (int j = 0; j < height; j++) 	      { 	         //calculate the vertical sampling indices 	         int sample_j0 = (j / samplePeriod) * samplePeriod; 	         int sample_j1 = (sample_j0 + samplePeriod) % height; //wrap around 	         float vertical_blend = (j - sample_j0) * sampleFrequency; 	  	         //blend the top two corners 	         float top = Interpolate(baseNoise[sample_i0][sample_j0], 	            baseNoise[sample_i1][sample_j0], horizontal_blend); 	  	         //blend the bottom two corners 	         float bottom = Interpolate(baseNoise[sample_i0][sample_j1], 	            baseNoise[sample_i1][sample_j1], horizontal_blend); 	  	         //final blend 	         smoothNoise[i][j] = Interpolate(top, bottom, vertical_blend); 	      } 	   } 	  	   return smoothNoise; 	} 	 	public float Interpolate(float x0, float x1, float alpha) 	{ 	   return x0 * (1 - alpha) + alpha * x1; 	} 	 	public float[][] GeneratePerlinNoise(float[][] baseNoise, int octaveCount) 	{ 	   int width = baseNoise.length; 	   int height = baseNoise[0].length; 	  	   float[][][] smoothNoise = new float[octaveCount][][]; //an array of 2D arrays containing 	  	   float persistance = 0.5f; // default value is 0.5f 	  	   //generate smooth noise 	   for (int i = 0; i < octaveCount; i++) 	   { 	       smoothNoise[i] = GenerateSmoothNoise(baseNoise, i); 	   } 	  	    float[][] perlinNoise = new float[width][height]; 	    float amplitude = 1.0f; 	    float totalAmplitude = 0.0f; 	  	    //blend noise together 	    for (int octave = octaveCount - 1; octave >= 0; octave--) 	    { 	       amplitude *= persistance; 	       totalAmplitude += amplitude; 	  	       for (int i = 0; i < width; i++) 	       { 	          for (int j = 0; j < height; j++) 	          { 	             perlinNoise[i][j] += smoothNoise[octave][i][j] * amplitude; 	          } 	       } 	    } 	  	   //normalization 	   for (int i = 0; i < width; i++) 	   { 	      for (int j = 0; j < height; j++) 	      { 	         perlinNoise[i][j] /= totalAmplitude; 	      } 	   } 	  	   return perlinNoise; 	} 	 	float[][] MapGray(float[][] perlinNoise) 	{ 	   int width = perlinNoise.length; 	   int height = perlinNoise[0].length; 	   float[][] image = new float[width][height]; 	   int ta=0, tr=0, tb=0, tg=0; 	   for (int i = 0; i < width; i++) 	   { 	      for (int j = 0; j < height; j++) 	      { 	    	  ta = 255; 	    	  int u = (int)(perlinNoise[i][j] * (float)80.0); 	    	  tr = u+100; 	    	  tg = u+100; 	    	  tb = u+100; 	    	  //ta = (int)(255.0f * perlinNoise[i][j]); 	    	  image[i][j] = (ta << 24) | (tr << 16) | (tg << 8) | tb; 	    	   	      } 	   } 	    	   return image; 	} 	 	float[][] MapGradient(float[][] perlinNoise) 	{ 	   int width = perlinNoise.length; 	   int height = perlinNoise[0].length; 	   float[][] image = new float[width][height]; 	   int ta=0, tr=0, tb=0, tg=0; 	   for (int i = 0; i < width; i++) 	   { 	      for (int j = 0; j < height; j++) 	      { 	    	  ta = 255; 	    	  int u = (int)(perlinNoise[i][j] * (float)angryFireColorTable.length); 	    	  tr = (int)angryFireColorTable[u][0]; 	    	  tg = (int)angryFireColorTable[u][1]; 	    	  tb = (int)angryFireColorTable[u][2]; 	    	  image[i][j] = (ta << 24) | (tr << 16) | (tg << 8) | tb; 	      } 	   } 	    	   return image; 	}  }